| Self-Organized Criticality | 2008-07-05 00:08 1 comment |
 by Flemming FunchSelf-Organized Criticality (SOC) is a theory about some principles that seem to pervade nature and which seems to explain various kinds of complexity very well. One of the most clear explanations is found in the book How Nature Works, by Per Bak, a Danish theoretical physicist who had an important role in developing the theory. SOC has been applied within a great number of disciplines, but it seems to remain a controversial subject for many scientists. You can guess that from looking at the reviews on Amazon for the book I just mentioned. Half the people absolutely love it, and the other half are bending over backwards to try to discredit it. It is indeed terribly ambitious to try to present a principle that covers so many natural phenomena. The mere attempt of doing so will rub anybody the wrong way who favors reductionism, i.e. reducing the world to smaller pieces that follow clearly defined laws that can be observed repetitively in clearly defined ways. Could of course also be bacause Bak was a pretty obnoxious character who didn't hesititate to tell other scientists off. Self-Organized Criticality says basically that there are certain dynamic systems that have a critical point as an attractor. I.e. that they "by themselves" will move towards a critical state. There are certain characteristics to such a system, but more about that in a moment. What is a critical state? Well, I'm no scientist, so I can't do much better than giving a very popularized version. It means very specific things in different scientific disciplines. It describes some kind of phase boundary, the border between several very different states. In simple language, something is on the edge, where interesting things happen when you push it in one direction or another. One can engineer various kinds of systems into being in a critical state, by fine-tuning the parameters. What's interesting about an SOC system is that the critical state happens naturally, in a way that's very robust, and doesn't change even if one changes the conditions. You find Self-Organized Criticality at play in natural systems such as earthquakes, avalanches, coast lines, evolution, weather patterns, neuro biology, cosmology, etc. Interestingly, you also find them in human systems such as in traffic patterns, population distribution, market prices, language patterns, in social networks, etc. We often assume that nature is in an equilibrium. Parts of it is. Something keeps the salt levels in the oceans at a stable level, something maintains the proper percentage of oxygen in the atmosphere. But, per definition, an equilibrium doesn't change. You push it and it tends to go back to the way it was. But the forces in nature that do more interesting things, that drive the great diversity, that create change and evolution, that's quite a different matter. That's where we find the self-organizing criticality.  One of the most simple examples is a pile of sand. Let's say that I drop grains of sand on the ground. At first nothing much happens, the new grains just pile on top of the old ones. But piles are then forming, getting higher, and at some point the slope will be steep, and the weight of the grains at the top will overcome the friction, and avalanches will start happening. Sometimes small avalanches, sometimes big avalanches. At some point the whole pile of sand will be in a critical state. Which just means that it is hovering at the edge of something happening, and exactly what will happen and when is difficult to know. You drop another grain of sand and maybe nothing happens, maybe it makes a few other grains tumble down, or maybe the whole pile will collapse. Whenever these sand slides happen, the system will again end up in another critical state.
There are several important characteristics to a system in an SOC state: - power laws - fractal geometry - 1/f (pink) noise A power law is basically any relationship between two variables where one is a power of the other. Another way of saying it is that it is a straight line in a double logarithmic coordinate system. The graph on the left is in a normal coordinate system, the graph on the right shows the same data in a logarithmic scale.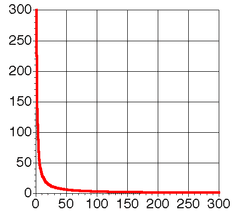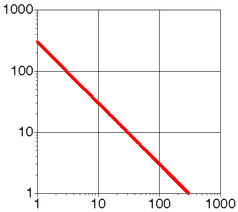  
A more simple way of saying it in relation to SOC is that small things happen very frequently and big things happen very rarely. And not just very rarely, but increasingly very, very rarely, the bigger they are. Since the Richter scale for earthquakes is fairly well known, that's a good example.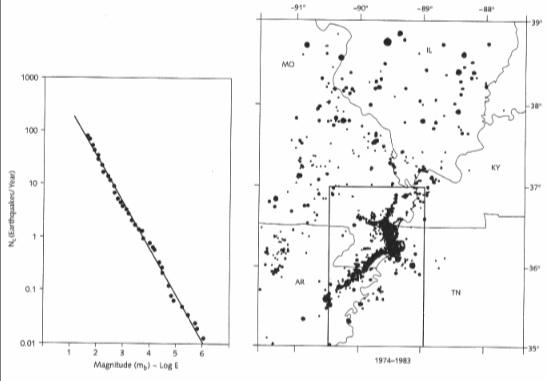 
Here you see, to the right, the distribution of earthquakes in a certain region over a certain period of time. Bigger dots are bigger earthquakes. If we plot the size of earthquakes against their frequency, and we put that on a double logarithmic piece of paper, we get something like what you see on the left. The richter scale is logarithmic. An earthquake of size 5 isn't just a bit bigger than a size 4, but it is a number of times bigger. It is slightly complicated, but you can remember that whenever you add 2 to the Richter number, 100 times more energy is let loose. I.e. a magnitude 6 earthquake has 100 times more energy than a magnitude 4. A magnitude 8 has 100 times more energy than a magnitude 6. That's basically a logarithmic scale for you there. The nice straight line that you see, that shows the power law. It is a distribution. It can show, for example, that for a certain magnitude X, you would find 4 times as many earthquakes with a magnitude of 1/2 of X. And you'd find 4 times fewer earthquakes with a size of 2 times X. I'm over-simplifying. You see this kind of relationship in many places. A fellow named Zipf studied linguistics, and he also did a study of the population of different cities. This is one of his graphs: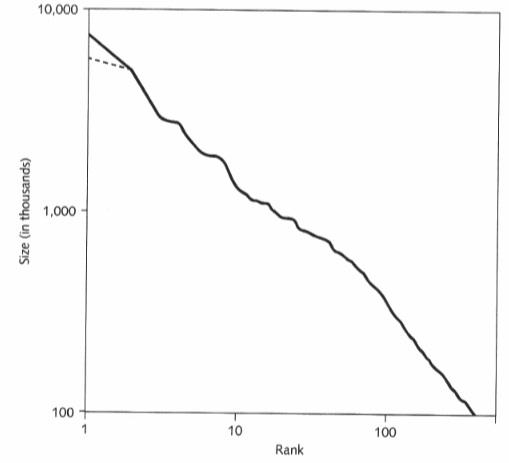 
Again, the same kind of thing. Take a certain size, like 1 million inhabitants. If we have X of those, there would be 4 times as many that would have 1/2 the size, i.e. 500 thousand. And there would 1/4 as many that would would have 2X the size, i.e. 2 million. That's a power law again. That phenomenon is also called scale-invariance. It basically means that there's no "normal" size of earthquakes or avalanches or cities or friend lists in social networks. There are many small ones and few big ones. No matter which part of the graph you look at, the pattern is the same. In principle, whether you look at cities with 1000 in habitants or 1 million, there will be the same formula for finding out how many you're likely to find with 1/2 the size or twice the size. In principle. In real life there are often upper or lower boundaries. You can't have any cities with a population larger than the number of inhabitants on the planet, or any with less than 1 inhabitant. 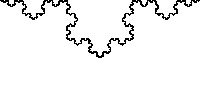 Fractal geometry is another characteric of self-organized critical systems. A fractal pattern is self-similar. Similar things go on no matter what scale you look at. In principle there's also an infinite amount of detail. You find fractal geometry in the flow of rivers, in coast lines, in the shape of mountains, trees, etc, and those are SOC.
 Pink Noise, aka 1/f noise, aka fractal noise, is another characteristic. Pink noise is often found in nature and tends to be the most pleasing of several kinds of noise. "Noise" applies to sound, obviously, but not just to sound. In this context we could just as easily call it "signal" as "noise". The reason it also is called 1/f is that the frequency (f) is inversely proportional to the power. Our taste for what is musical tends to follow such a principle, where each octave has the same energy, and our musical scale is a logarithmic scale. Pink noise is a signal (or a noise) where all sorts of frequencies are mixed, where the low (slow) frequencies are strong, and the high (fast) frequencies are weak. Or, seen the other way, there is a lot of small things going on, and few big things. This all sounds more complicated than it is. It is really just another way of saying something similar to what the power law says, or what fractals say.
Imagine a flowing river. The overall current is a strong low-frequency flow. Within that there is a great frequency of small flows, the eddies in the water. Not very strong each of them, but there are many of them. Within the river there are both the few strong flows that don't change quickly, and the many weak flows that change all the time. And there's everything in-between. Distributed exactly by a power law, exhibiting fractal geometry, and it would sound like pink noise, exactly because the activity is distributed that way. If you look at a graph of, say, stock market fluctuations: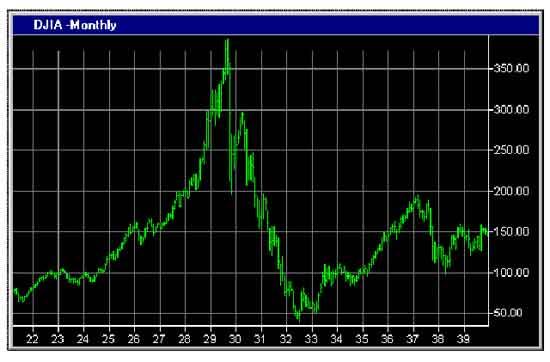 
You see this kind of thing. There are big slow moving frequencies with many small and fast fluctuations in-between. Many frequencies mixed together, of different magnitude. Back to SOC. One of the important discoveries about self-organizing critical systems is that they can be simulated quite well with cellular automata. Similar to how fractals can be generated with simple recursive formulas.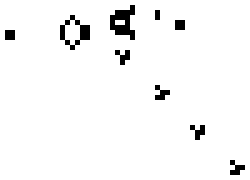 
A cellular automaton is in its most simple form that you make a grid of cells and you establish some simple rules about how the state of one cell depends on the state of the cells around it in the previous round. The most famous example is Conway's Life Game. These are its rules: 1. Any live cell with fewer than two live neighbours dies, as if by loneliness. 2. Any live cell with more than three live neighbours dies, as if by overcrowding. 3. Any live cell with two or three live neighbours lives, unchanged, to the next generation. 4. Any dead cell with exactly three live neighbours comes to life. From those simple rules, wonderous phenomena come to life, as seen in the picture above. Similar simulations can be used to illustrate SOC phenomenon. Let's say the avalanches in a sand pile.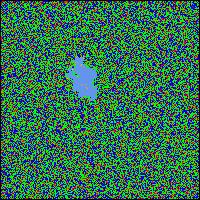  
 
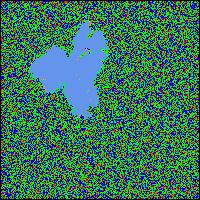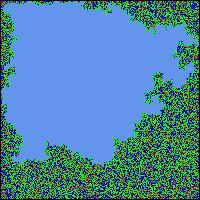
We simplify things greatly and say that piles of sand can have a height of between 0 and 3 grains. They're shown with the colors gray, green, blue and red for a height of 0, 1, 2 and 3 respectively. We establish the simple rule that once a pile has 3 grains and we add another, the pile will tumble and the 4 grains will be distributed to the 4 neighboring cells. If some of those piles already had 3 grains, they might tumble as well, etc. In each round we basically just drop a grain of sand in a random place, and we see what happens. If we had started with an empty grid, it would be a while before much will happen. The first picture essentially shows a grid that already has reached a critical state. To a human eye, the simulation in a critical state doesn't look any different from a random distribution of grains. But it is. It is essentially already wound up and ready to go. When we drop another grain of sand, nothing might happen, a small avalanche might happen, or a huge avalanche might happen. The power law distribution again. The 3 following pictures show the development of an avalanche, in blue. We dropped just one grain, but it toppled some piles which toppled some other piles, and the chain reaction continued for a while until a large portion of the cells have been involved at least once. The point about a critical state is that it is not at all obvious what will happen when we touch it. It is a state where something is likely to happen, but there is no simple formula for predicting exactly what. It might sound like we're only talking about bad things happening, like avalanches. However, very similar mechanisms are in place in everything from evolution of species to traffic patterns on freeways to the connections between neurons in your brain. Some evolutionary biologists have made the mistake of assuming that evolution happens gradually at an even speed all the time. It doesn't really, as the fossil record shows. Species might exist largely unchanged for millions of years, and suddenly, in a relatively short period of time, lots of changes happen. Many species go extinct, many others evolve into new forms rather quickly. That's called punctuated equilibrium, and is entirely consistent with the self-organized criticality principle. Small things happen often, and they might be so small that it looks like equilibrium. Big things happen so rarely that they might look like unprecedented catastrophes. If you chart the number and frequency of extinctions, you get a power law. You don't need any big external event like a meteor to explain the mass extinctions in the past. Or, rather, it doesn't matter if was a meteor or something else, the patterns are more or less the same. Evolution can be simulated quite well with cellular automata as well. It might be hard to visualize what a state of criticality is about. Since it applies to social networks between humans as well, it might be useful to develop some metaphors and try to understand it better. An early experiment that Per Bak did with his partners involved pendulums and watch springs. It was a fairly complicated thing where one could rotate the pendulums around an axis, which would wind up some of the springs, and the springs would be what connected each pendulum to the next, in a grid, so that each pendulum would be connected with four others through four springs, if I understand it right. When you first twist a pendulum around, nothing happens. But as you gradually have rotated many pendulums several times, and wound up many of the springs more and more, at some point you've brought this whole system into a critical state. A state where when you rotate one more pendulum, you set off a chain reaction. The one pendulum sets off another tightly wound pendulum, which in turn sets off others. Again, most of the time the chain reaction is small, but sometimes the whole system takes off. The metaphor of watch springs seems useful. You can think of a critical system as one where all the pieces are wound up. At the same time, you don't know exactly how it is wound up, so you don't know what will happen when you poke it somewhere. But something is likely to happen. SOC is the most efficient way a dynamic system can organize itself. It is not necessarily the most efficient way one deliberately can organize something, but it is the most efficient way it can organize itself. SOC is an example of complexity. Complexity in the sense of a system where the sum is more than the parts, a system which will behave in ways that we couldn't easily predict from studying the parts. You don't just have a bunch of pieces. You have pieces that have developed a complex pattern of relations between them. A pattern where many parts of the system are ready to be triggered and potentially affecting a big portion of the whole system. The pieces are wound up and they're connected with other pieces that are also wound up. We could use the metaphor of dominos that are lined up and ready to fall if you push one of them. But it is more complex than that. You could relatively easily see which domino to push and approximately what will happen. In an SOC system everything is connected in a much more intricate way and different things will happen depending on where you push it. We might over-simplify things for our purposes and say that there are three kinds of states of a system: - equilibrium - criticality - chaos If you poke at a system that is in equilibrium, nothing much happens. Or, if something happens to it, it would tend to go back to the same state as before. If you poke at a system that is in chaos, something random will happen. If you poke at a system that's bordering on chaos, obviously something very random and chaotic might happen. If you poke at a system that is complex, in particular one that is self-organized criticality, something is likely to happen. Probably something small, but maybe something big. Despite that we've talked about avalanches and earthquakes, it should be stressed that the critical state is not chaos. It is not just some random catastrophe. It is ordered, although not in a way that's very transparent to us humans. The critical state is also robust. It is always on the edge, but the edge is stable, although changing.  That might be hard to wrap one's mind around. Think about a wave in the ocean. It is neither in equilibrium nor is it chaotic. It is critical. It is the edge. There are small waves and big waves. They're all connected. If you watch a particular wave, it is moving, but it remains coherent as a wave, at least until it eventually crashes on the beach. If you're a surfer, you can catch a good wave and ride on it. When you're done with it, you can catch another. Waves are not random, they don't just come out of nowhere. You might not understand exactly how a wave came about, but you can learn to have a sense of whether one is coming, and you can catch it.
Social networks seem to self-organize towards criticality. They follow power laws. There are many small events and few big events. All sorts of frequencies are mixed together. There's a relatively pleasing pink noise. The network dynamically self-organizes itself into the most efficient state it could, without anybody being in charge. Many relationships have formed. The many actions of many individuals have woven a web of complexity. The network has over time become wound up in many ways.  So, in a complex social network, if you do something, something might happen. Something is more likely to happen than if all connections were random, or if it was neatly ordered in some very balanced way. Mostly small things happen, but there's an opportunity for big things to happen. You drop a message to somebody else, and if it is the right kind of message at the right time, the network is ready to allow a chain reaction to happen. Millions of people might be talking about it tomorrow. No guarantees, but the network is ready for you.
We ought to understand all of this better, of course. It seems to be a human tendency to try to fight against it. Central banks try to keep the economy in a perpetual equilibrium. Industrialized farming tries to grow just the crops we think we want, and nothing else. We try to organize things so that nothing bad ever happens. But we might at the same time be sabotaging the mechanisms that allow great things to happen. We might need to learn to surf on the edge of the wave of complex change, rather than seek in vain the safety between the waves. |